I entered Anne of Green Cables in Interactive Fiction Comp 2025 where it got a respectable 25th place out of 85. It’s an interactive story mashing up the pastoral classic with a solarpunk twist. You can play it for free on itch.io.

The finale of the game involves a minigame puzzle. I wanted to walk through some of my design for this, because I think it’s currently one of my personal best bits of puzzle design. Although the puzzle is simple, there’s a surprising depth of mathematics behind it, and some narrative design.

The puzzle

Without getting into too deep into the story, the CEO of StrataCorp is strong-arming Anne Shirley into signing over the ownership of her community. They are trying to change the cooperative community into a corporate asset to sell off. The actual exchange is through something like a cryptocurrency coin tumbler: mix up the entities and redistribute them to the owners. The CEO is trying to do a shell game with your community to avoid legal scrutiny.

But he’s messed up. Anne has managed to get her hacker crowbar into the contract and change the order of the mixers. Is this enough for her to change a horrible situation into a good one?

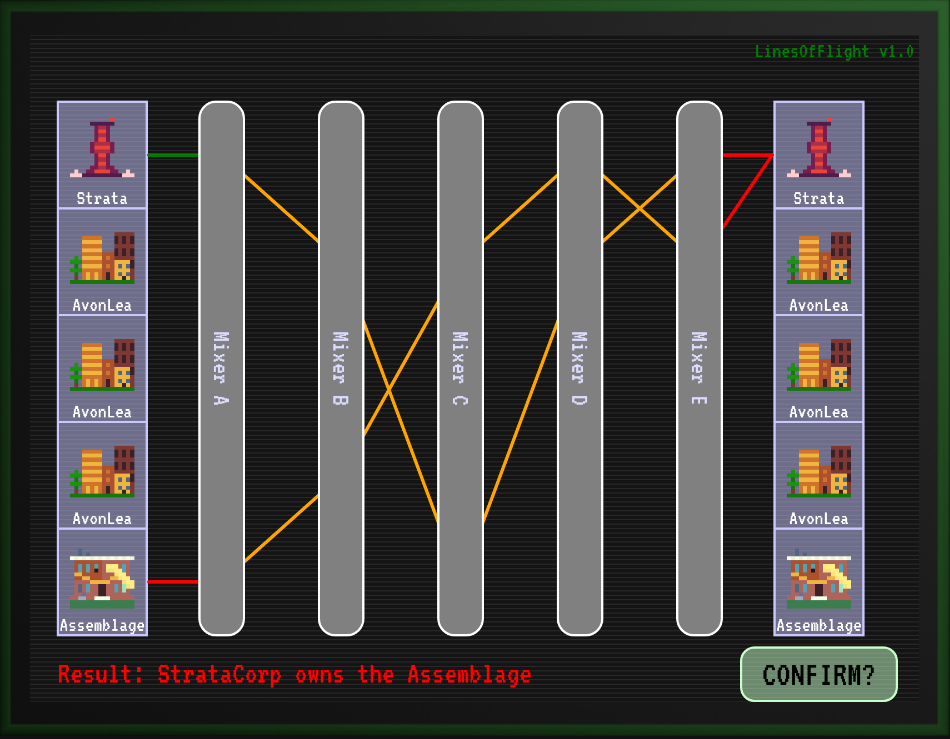
The initial setup has Strata and The Assemblage (the community centre) going into some mixers. These shuffle the assets around until they converge into the Strata bin, which is a bad result.

You can see the solution in action:

As you shuffle the mixers around you can watch where the assets go. A bad result is indicated in red. An okay-not-great is in orange, and the ideal (steal everything from the bad guys) is in green.

Each mixer is deterministic, but their order is the important factor. There are five ports in each and they map to the next five ports. Sometimes they permute the assets about. Sometimes they group them together.

The minigame is styled in upscaled pixel art with some screen artifacts to emulate the puzzle being on a bespoke computer made by resourceful hackers.

The theme

Throughout Anne of Green Cables I snuck in the theme of deterritorialization from philosophers Deleuze and Guattari, which is roughly how structures in society change when contexts are changed. Anne’s journey from orphan to community leader doesn’t change her fundamentally — she continues to be an imaginative, hot-headed girl — but the context in which she is considered and how she thinks of herself changes, and this changes the community as well.

Even the meta-story itself is a form of this philosophy: the game is roughly the classic novel Anne of Green Gables but in a cyberpunk world, which changes the context and how you might understand the original.

I wanted a puzzle to reflect this theme. I wanted the actions of the puzzle to be changing the context of a situation to effect a different outcome.

Cryptocurrency coin tumblers felt appropriately cyberpunk, but also encapsulated the theme I was looking for. While real tumblers are a lot more complicated, this was a nice abstraction.

There was also a sly nod to Deleuze and Guattari in the theming, as the hacking game was called “Lines of Flight” up in the right-hand corner and the puzzle space you explore is all the multiplicity of lines describing the deterritorialization of assets.

Helpful flourishes

Abstract puzzle games are great, but it can help to subtly signal information to the player.

The lines in the mixers show where inputs go and it looks a little like they refract through the mixers like prisms. They highlight red, orange or green depending on where they hit the goals at the end. The crutch that “green is good” can help a player instinctively search for a solution.

Although there’s some oddity with very steep angles, the lines always point to one of five spots in the middle of the mixer. In this way you can take notes on where an input maps to.

If you hover over a mixer, it shows a strong path from the left (the past) and then weak paths to the right (the future). If you pick up a mixer, the paths truncate appropriately.

A moving mixer is smaller than the stationary ones. If you’re about to drop a mixer into a position, that position lights up so you know where it’s going to go. There’s some leeway in that so you don’t need to be exact. When you shift them into place, they all slide to their final positions.

There’s a big green button for you to confirm your pick, there’s no timer and you can experiment as much as you like. There’s also a link in the text to an overview of how the puzzle works, and also a simple “Skip the puzzle” where you can just select your ending explicitly. At the end of a long story game, people might just want to see the end.

The meaning of the result is included at the bottom as text (eg “Result: StrataCorp owns the Assemblage”) and updates automatically. It is colour-coded on whether it’s a good, bad or ambiguous ending.

Parameters of the puzzle

There are two fixed ends, the input nodes and the output nodes. They are the same entities: StrataCorp (bad), Assemblage (good) and AvonLea (neutral). We have only five entities and the general idea is to mix the good and the bad in with the neutral and see what comes out.

There are four separate “win” states:

1. The Assemblage goes to StrataCorp (bad)
2. The Assemblage goes to StrataCorp and AvonLea (less bad but still bad)
3. StrataCorp instead is the one split up between The Assemblage and AvonLea (pretty good)
4. StrataCorp goes entirely to The Assemblage (best)

So there’s win states for all bad, all good and somewhere in between. It is possible for all assets to go to AvonLea, which counts as win type 3. It is impossible for all assets to return to StrataCorp and The Assemblage simultaneously.

There are five mixers. Each mixer can take a signal from the five input ports, and send them to any of the five input ports of the next mixer or end point.

The initial input of assets (StrataCorp and The Assemblage) are fixed.

Each mixer is different, and each mixer changes something.

Note that we have to think about the mixers as taking sets of inputs and producing sets of outputs. The first input set is \(\{1,5\}\) and in the initial bad guy configuration it ends up as the set \(\{1\}\). The good guy goal is a final set of \(\{5\}\).

If you’re taking notes on the mixers, there are five parameters of data per mixer: what input goes to what output. So that’s 25 data points altogether, which isn’t too bad.

If there were more places (say a couple of Strata and more AvonLeas), then this increases the note-taking significantly. If there are more mixers, there are many more combinations and brute force quickly becomes infeasible. So the magic number 5 for both number of places and number of mixers is in a sweet spot. 6 would also be okay, I feel. My original attempt had 5 mixers and 15 asset locations.

The mathematics of solving the puzzle

How hard is this puzzle? There are five mixers in some order and this is all the player can mess with. Mixer A can go in any of the five places, then Mixer B in any of the four remaining places, Mixer C in any of the remaining three places, Mixer D in any of the two remaining places, and that leaves Mixer E in whatever’s left. There are therefore \(5! = 5 \times 4 \times 3 \times 2 \times 1 = 120\) combinations. With a good scheme to get through all orderings, a player could conceivably just brute force your way through in a few minutes by hand. It’ll take on average 60 checks to find the solution amongst the 120 permutations.

120 total permutations is enough that you probably won’t stumble across it by accident too quickly. We want there to be a single solution. It turns out as we’ll see that there’s actually a few and it’s structurally hard to avoid this.

The mathematics of designing the mixers

There are two types of mixers under consideration: permutations and condensers. A permutation will take the input set \(\{1,2,3,4,5\}\) and produce the set \(\{1,2,3,4,5\}\) in some order. Permutations reorders things, in other words. It doesn’t lose or gain any. A condenser will not produce the set \(\{1,2,3,4,5\}\), typically because it has mapped two inputs to the same output. We need condensers to allow for the good and bad win states.

You could instead repeat the Strata and Assemblage positions so that instead of assets converging at a point, they are only permuted and hit the same type of output (all StrataCorp, for example). This is equivalent to using condensers, but it makes it messier to reason about as we start constructing our mixers.

Also importantly, a mixer won’t turn an input set of N things into more than N things, and won’t turn them into zero things, because that would be weird and mess with our design in many ways. It’d also make it slightly harder to program.

There are 120 different permutation mixers (input 1 goes to one of \(\{1,2,3,4,5\}\), input 2 goes to one of the remaining, etc). By framing condensers as the exclusion of permutations, we can count them easily: each input gets free choice of where they go so that’s \(5^5 = 5 \times 5 \times 5 \times 5 \times 5 = 3125\) mixers in total, but if we subtract off the 120 permutations we have \(3125-120 = 3005\) condensers.

Can we get a set of five different mixers such that:

1. The initial ordering maps \(\{1,5\}\) to {1} (bad guys win solution)
2. There exists at least one ordering such that \(\{1,5\}\) maps to \(\{5\}\) (good guys win solution)
3. There are no orderings that map \(\{1,5\}\) to \(\{1,5\}\) (both good and bad guys win solution)
4. Requirements 1, 2 and 3 mean there must be at least one condenser mixer.
5. There are not too many bad guy or good guys solutions.

Since there are \(3125\) different mixers, we have \(3125 \times 3125 \times 3125 \times 3125 \times 3125 \approx 2.9 times 10^17\). In bits this is about \(2^58\), which is in the ballpark of cracking the DES cryptosystem. Jeepers! We better rethink this.

Okay, so a blind brute force won’t work. We can introduce some subtle structure to the mixers to make our search easier, but not ruin the puzzle.

The first thing is inverse permutation mixers. For a permutation \(A\), there is necessarily another permutation \(A^{-1}\) that undoes that permutation. They are called inverses of each other. So if like in the final solution \(A\) and \(D\) are inverses of each other, then this effectively reduces the puzzle down to three mixers because if you place \(A\) before \(D\) (or the other way around), they cancel each other out. This is a nice little “Aha” moment for a player because they can divide-and-conquer.

I didn’t want any of the mixers to be equal, so this cuts out any permutation that is its own inverse. There are 26 of them, including the identity permutation which maps an input identically to its output.

If I choose a random permutation with an inverse, then we have \(120-26=94\) choices for that permutation, and no choices for its inverse. That’s \(94 \times 3125 \times 3125 \times 3125 = 2.8 \times 10^{12}\) options to cycle through, which is a lot better.

One trick is that if Mixer A and Mixer B are inverses, then I can put them as a pair anywhere I like: (AB)CDE, C(AB)DE, CD(AB)E, and CDE(AB) are all the exact same result: CDE. So if there is one solution, there are four. This is less nice for our puzzle design aesthetics, but it doesn’t trivialise the problem.

Heuristically the remaining 3 mixers can’t be freely chosen mixers because of constraints like our initial condition. For example, one of the mixers (say E) has to send inputs to \(\{1,5\}\). Then one of the mixers (say D) has to send its inputs to the inputs that E will map to \(\{1,5\}\). And then C’s will have to send the initial input (\(\{1,5\}\)) to the right places in D which sends them to the right places in E to go to \(\{1\}\). Then you mix CDE up to the “good guys win” scenario and run the same logic. There isn’t that much choice.

Similarly we likely can’t have three condensers C, D, E because that directs the paths too much, which interacts with our other puzzle requirements.

A nice compromise is to choose two of C, D, E to be permutations and one as a condenser. This confines the weird but required condenser behaviour to a single mixer. This is an extra bit of leverage for the player.

Even with this, the permutations C and D still have to obey the heuristics and not mess up our structure from A and B. For example, C can’t secretly be the permutation A or B, because that collapses the outcomes too much and if there happens to be a good guys solution, there’ll be way too many.

At this point I wrote a modestly clever brute force searcher, using all the above information to quickly discard putative solutions. I also made it easier to evaluate options: the initial ABCDE bad guy configuration had to have a particular result, and I chose the solution (AD)CBE (and the other equivalent solutions) to be the good guy configuration. This was a few moves away from the initial configuration so it wasn’t easy to stumble across it.

For each configuration you need to evaluate every ordering and get statistics on the number of good/bad/neutral solutions. This ran overnight and gave me a few solutions. The puzzle aesthetics really cut down the number of options to a manageable level.

End product

I wrote the minigame in p5.js which was easy to integrate into Twine, the system the rest of the game uses. With a little bit of animation, colour and nice pictures, it worked as a minigame. While it wasn’t the world’s most compelling puzzle, I think it hit a sweet spot of puzzle complexity versus user simplicity, as well as tying into the narrative.

p5.js gives you the ability to include information for screen-readers. I did as much as I could for this, but its a lot of information to describe and I don’t think anyone used it.

There were additions that I had considered but not implemented. For example, tracking the information that a player has seen and displaying it visually. Instead of bright coloured lines, maybe they are in grey. Perhaps the AvonLea inputs are mapped through as far as they can go with your knowledge, so you’re seeing information like “Oh okay, if I can get an input of 3 into Mixer C, then that maps to…” and allow the player to reason about what they are seeing. A player can build up a full visual table of what the mixers are doing without doing the paperwork themselves.

Apart from implementing this addition, I worry that it swiftly makes the puzzle noisy-looking. It is nice to give players as many affordances as you can, though.

All in all, I was pleased with the results, it worked and a number of players enjoyed it.